

 | Procedure Division | Procedure Division - ACCEPT - DIVIDE |  |
![]()
The Intrinsic Function module allows you to reference a data item whose value is derived automatically at the time of reference during the execution of the object program.
If your program uses intrinsic functions, you will also require the floating-point module. See your COBOL system documentation about building and linking for details of run-time system support modules.
In the Intrinsic Function module, a function is a temporary data item whose value is determined at the time the function is referenced during the execution of a statement. A function-name is a COBOL word that is one of a specified list of COBOL words which can be used in COBOL source programs. (See the section Definitions of Functions later in this chapter.)
The definition of each function specifies:
![]() and national
and national
functions, the size of the returned value
A function-identifier is used by the programmer to reference a function in the Procedure Division of a COBOL source program. (See the section Function-Identifier in the chapter Concepts of the COBOL Language.)
The value returned by a function is considered to be a data value. A mechanism is provided at run time to assign a data value to a function when it is referenced. In order to determine the function's value, the evaluation mechanism requires access to data values provided by the referencing program. These data values are provided by specifying parameters, known as arguments, when referencing the function. Specific functions can place constraints on these arguments, such as range, and so on. If, at the time a function is referenced, the arguments specified for that reference do not have values that comply with the specified constraints, then the returned value for the function is undefined.
Arguments specify values used in the evaluation of a function. Arguments are specified in the function-identifier. These arguments can be specified as identifiers, as arithmetic expressions, or as literals. The definition of a function specifies the number of arguments required, which can be zero, one, or more. For some functions, the number of arguments which can be specified is variable. The order in which arguments are specified in a function-identifier determines the interpretation given to each value in arriving at the function value. Arguments may be required to have a certain class or a subset of a certain class. The four types of argument are:
The rules for a function can place constraints on the permissible values for arguments, in order to accurately determine the function's value. If, at the time a function is referenced, the arguments specified for that reference do not have values within the permissible range, the returned value for the function is undefined.
When the definition of a function permits an argument to be repeated a variable number of times, a table can be referenced by specifying the data-name and any qualifiers that identify the table, followed immediately by subscripting where one or more of the subscripts is the word ALL.
When ALL is specified as a subscript, the effect is as if each table element associated with that subscript position were specified. The order of the implicit specification of each occurrence is from left to right, with the first (or leftmost) specification being the identifier with each subscript specified by the word ALL replaced by one, the next specification being the same identifier with the rightmost subscript specified by the word ALL incremented by one.
This process continues with the rightmost ALL subscript being incremented by one for each implicit specification until the rightmost ALL subscript has been incremented through its range of values. If any additional ALL subscripts exist, the subscript immediately to the left of the rightmost ALL subscript is incremented by one, the rightmost ALL subscript is reset to one and the process of varying the rightmost ALL subscript is repeated. The ALL subscript to the left of the rightmost ALL subscript is incremented through its range of values. For each additional ALL subscript this process is repeated in turn until the leftmost ALL subscript has been incremented by one through its range of values.
If the ALL subscript is associated with an OCCURS DEPENDING ON clause, the range of values is determined by the object of the OCCURS DEPENDING ON clause. The evaluation of an ALL subscript must result in at least one argument, otherwise the result of the reference to the function-identifier is undefined.
01 Test-Fields.
10 OT-Elem PIC 9(02).
10 Arr.
15 Ind occurs 5 times PIC 9(02).
compute OT-Elem = function sum (IND(ALL)).
is equivalent to specifying
compute OT-Elem = function sum (IND(1), IND(2), IND(3),
IND(4), IND(5)).
The ALL subscript can also be used with a table that has a variable number of elements as in the following example:
01 Test-Group.
03 OT-Elem pic 9(15) binary.
03 table-length pic s9(9) binary.
03 array.
05 Ind pic 9(2) occurs 1 to 200 times depending on
table length
...
move 100 to table-length.
compute OT-Elem = function sum (Ind(ALL))
These statements will sum the first 100 elements of the table. At the time the function is referenced, the number of elements specified by table-length determines that number of elements that are added.
Data item functions are elementary data items and return alphanumeric,
![]() national,
national,
numeric or integer values. Data item functions are treated as elementary data items and cannot be receiving operands. The three types of data item functions are:
![]() or as the source of
a MOVE statement.
or as the source of
a MOVE statement.
![]() or as the source of
a MOVE statement.
or as the source of
a MOVE statement.
The Gregorian calendar is used in the date conversion functions. The starting date of Monday, January 1, 1601, was chosen to establish a simple relationship between the Standard Date and DAY-OF-WEEK; that is, the integer date 1 was a Monday, DAY-OF-WEEK 1.
For example, the statement:
compute DoW = function rem (function integer-of-date (date-field) , 7)
returns the day of week for a given date, where 0 is Sunday, 1 is Monday, and so on.
Trigonometry deals with the relationships among the sides of a triangle and its angles. An angle can be measured in degrees, radians or Gon (grad). Since a computer usually generates trigonometric values by series approximation, the angle is specified in radians when used as the argument to the SIN, COS, and TAN functions or as the returned value fromthe ASIN, ACOS, and ATAN functions.
A radian is an arc of a circle whose length is equal to the circle's
radius. Since the relationship between a circle's radius and circumference
is C = 2 * P * r, and there are 360 degrees in a
circle, we can derive from 360 = 2 * P * r, that the
values for conversion are:
1 radian = 180/P = 57.295780 degrees
1 degree = P/180 = 0.01745329 radians.
Another scale that is sometimes used to measure angles is Gon, also known as grad. The values for conversion are:
1 radian = 200/P = 63.661977 Gon (grad)
1 Gon (grad) = P/200 = 0.01570796 radians.
The following table summarizes the functions that are available.
The "a rguments" column defines argument type and the "type" column defines the type of the function, as follows:
| Alph | means alphabetic |
| Anum | means alphanumeric |
| Int | means integer |
|
|
means national |
| Num | means numeric |
| Function-Name | Arguments | Type | Value Returned |
|---|---|---|---|
|
|
Int1 or Num1 | Depends upon arguments | The absolute value of argument |
| ACOS | Num1 | Num | Arcosine of Num1 |
| ANNUITY | Num1, Int2 | Num | Ratio of annuity paid for Int2 periods at interest of Num1 to initial investment of one |
| ASIN | Num1 | Num | Arcsine of Num1 |
| ATAN | Num1 | Num | Arctangent of Num1 |
| CHAR | Int1 | Anum | Character in position Int1 of the alphanumeric program collating sequence |
|
|
Int1 | Nat | Character in position Int1 of the national program collating sequence |
| COS | Num1 | Num | Cosine of Num1 |
| CURRENT-DATE | None | Anum | Current date and time and difference from Greenwich Mean Time |
| DATE-OF-INTEGER | Int1 | Int | Standard date equivalent (YYYYMMDD) of integer date |
| DATE-TO-YYMMDD | Int1 | Int | Argument-1 converted Int2 from YYMMDD to YYYYMMDD based on the value of argument-2 |
| DAY-OF-INTEGER | Int1 | Int | Julian date equivalent (YYYYDDD) of integer date |
| DAY-TO-YYYYDDD | Int1 | Int | Argument-1 converted Int2 from YYDDD to YYYYDDD based on the value of argument-2 |
|
|
Nat1, Anum1 | Anum | Usage display representation of argument Nat1 |
|
|
None | Num | The value of e, the natural base |
|
|
Num1 | Num | e raised to the power Num1 |
|
|
Num1 | Num | 10 raised to the power Num1 |
| FACTORIAL | Int1 | Int | Factorial of Int1 |
|
|
Num1 | Num | Fraction part of Num1 |
| INTEGER | Num1 | Int | The greatest integer not greater than Num1 |
| INTEGER-OF-DATE | Int1 | Int | The integer date equivalent of standard date (YYYYMMDD) |
| INTEGER-OF-DAY | Int1 | Int | The integer date equivalent of Julian date (YYYYDDD) |
| INTEGER-PART | Num1 | Int | Integer part of Num1 |
| LENGTH | Alph1 or Anum1 or or Num1 |
Int | Length of argument in number of character positions |
|
|
Alph1 or Anum1 or Int1 or Nat1 or Num1 | Int | Length of argument in number of alphanumeric character positions |
| LOG | Num1 | Num | Natural logarithm of Num1 |
| LOG10 | Num1 | Num | Logarithm to base 10 of Num1 |
| LOWER-CASE | Alph1 or Anum1 or |
Depends upon argument | All letters in the argument are set to lowercase |
| MAX | Alph1 ... or Anum1 ... or Int1 ... or Num1 ... |
Depends upon arguments* | Value of maximum argument |
| MEAN | Num1 ... | Num | Arithmetic mean of arguments |
| MEDIAN | Num1 ... | Num | Median of arguments |
| MIDRANGE | Num1 ... | Num | Mean of minimum and maximum arguments |
| MIN | Alph1 ... or Anum1 ... or Int1 ... or Num1 ... |
Depends upon arguments* | Value of minimum argument |
| MOD | Int1, Int2 | Int | Int1 modulo Int2 |
|
|
Anum1, |
Nat | Usage national representation of argument Anum1 |
| NUMVAL | Anum1 or |
Num | Numeric value of simple numeric string |
| NUMVAL-C | Anum1, Anum2, or |
Num | Numeric value of numeric string with optional commas and currency sign |
| ORD | Alph1 or Anum1 or |
Int | Ordinal position of the argument in collating sequence |
| ORD-MAX | Alph1 ... or Anum1 ... or Num1 |
Int | Ordinal position of maximum argument |
| ORD-MIN | Alph1 ... or Anum1 ... or Num1 |
Int | Ordinal position of minimum argument |
|
|
None | Num | Value of |
| PRESENT-VALUE | Num1 Num2 ... | Num | Present value of a series of future period-end amounts, Num2, at a discount rate of Num1 |
| RANDOM | Int1 | Num | Random number |
| RANGE | Int1 ... or Num1 | Depends upon arguments* | Value of maximum argument minus value of minimum arguments |
| REM | Num1, Num2 | Num | Remainder of Num1/Num2 |
| REVERSE | Alph1 or Anum1 or |
Depends upon argument | Reverse order of the characters of the argument |
|
|
Num1 | Int | The sign of Num1 |
| SIN | Num1 | Num | Sine of Num1 |
| SQRT | Num1 | Num | Square root of Num1 |
| STANDARD-DEVIATION | Num1 ... | Num | Standard deviation of arguments |
| SUM | Int1 ... or Num1 ... | Depends upon arguments* | Sum of arguments |
| TAN | Num1 | Num | Tangent of Num1 |
| UPPER-CASE | Alph1 or Anum1 or |
Depends upon argument | All letters in the argument are set to uppercase |
| VARIANCE | Num1 ... | Num | Variance of argument |
| WHEN-COMPILED | None | Anum | Date and time program was compiled |
| YEAR-TO-YYYY | Int1 Int2 |
Int | Argument-1 converted from Int2 YY to YYYY based on the value of argument-2 |
* A function that has only alphabetic arguments is type alphanumeric.
![]()
The ABS function returns the absolute value of the argument.
The type of this function is according to the argument type as follows:
| Argument Type |
Function Type |
|---|---|
| Integer | Integer |
| Numeric | Numeric |
![]()
The ACOS function returns a numeric value in radians that approximates the arccosine of argument-1. The type of this function is numeric.
![]()
Note: Conversion factors from radians to degrees and Gon (grad) are specified in the section Trigonometric Functions of this chapter.
The ANNUITY function (annuity immediate) returns a numeric value that approximates the ratio of an annuity paid at the end of each period for the number of periods specified by argument-2 to an initial investment of one. Interest is earned at the rate specified by argument-1 and is applied at the end of the period, before the payment. The type of this function is numeric.
![]()
1 / argument-2
argument-1 / (1 - (1 + argument-1) ** (- argument-2))
The ASIN function returns a numeric value in radians that approximates the arcsine of argument-1. The type of this function is numeric.
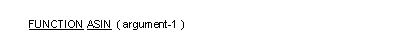
Note: Conversion factors from radians to degrees and Gon (grad) are specified in the section Trigonometric Functions of this chapter.
The ATAN function returns a numeric value in radians that approximates the arctangent of argument-1. The type of this function is numeric.
![]()
Note: Conversion factors from radians to degrees and Gon (grad) are specified in the section Trigonometric Functions of this chapter.
The CHAR function returns a one character alphanumeric value that is a character in the program collating sequence having the ordinal position equal to the value of argument-1. The type of this function is alphanumeric.
![]()
![]()
The CHAR-NATIONAL (national character) function returns a one-character value that is a character in the national program collating sequence having the ordinal position equal to the value of the argument.
The type of the function is national.
![]()
The COS function returns a numeric value that approximates the cosine of an angle or arc, expressed in radians, that is specified by argument-1. The type of this function is numeric.
![]()
Note: Conversion factors from degrees and Gon (grad) to radians are specified in the section Trigonometric Functions of this chapter.
The CURRENT-DATE function returns a 21-character alphanumeric value that represents the calendar date, time of day, and local time differential factor provided by the system on which the function is evaluated. The type of this function is alphanumeric.

| Character Positions |
Contents |
|---|---|
| 1-4 | Four numeric digits of the year in the Gregorian calendar. |
| 5-6 | Two numeric digits of the month of the year, in the range 01 through 12. |
| 7-8 | Two numeric digits of the day of the month, in the range 01 through 31. |
| 9-10 | Two numeric digits of the hours past midnight, in the range 00 through 23. |
| 11-12 | Two numeric digits of the minutes past the hour, in the range 00 through 59. |
| 13-14 | Two numeric digits of the seconds past the minute, in the range 00 through 59. |
| 15-16 | Two numeric digits of the hundredths of a second
past the second, in the range 00 through 99.
If the system does not have the facility to provide fractional parts of a second, the value 00 is returned. |
| 17 | Either the character "–", the
character " +", or the character "0". The
character "–" is returned if the local time indicated
in the previous character positions is behind Greenwich Mean Time.
The character "+" is returned if the local time indicated
is the same or ahead of Greenwich Mean Time. The character "0"
is returned if the system on which this function is evaluated does
not have the facility to provide the local time differential factor.
If the system does not have the facility to provide the local time differential factor, the value 00000 is returned in character positions 17 through 21. |
| 18-19 | If character position 17 is "–", two numeric digits are returned in the range 00 through 12 indicating the number of hours that the reported time is behind Greenwich Mean Time. If character position 17 is "+", two numeric digits are returned in the range 00 through 13 indicating the number of hours that the reported time is ahead of Greenwich Mean Time. If character position 17 is "0", the value 00 is returned. |
| 20-21 | Two numeric digits are returned in the range 00 through 59 indicating the number of additional minutes that the reported time is ahead of or behind Greenwich Mean Time, depending on whether character position 17 is "+" or "–" , respectively. If character position 17 is "0", the value 00 is returned. |
The DATE-OF-INTEGER function converts a date in the Gregorian calendar from integer date form to standard date form (YYYYMMDD). The type of this function is integer.
![]()
The DATE-TO-YYYYMMDD function converts argument-1 from the form YYnnn to the form YYYYnnn. Argument-2, when added to the year at the time of execution, defines the ending year of a 100-year interval, or sliding window, into which the year of argument-1 falls. The type of this function is integer.
FUNCTION DATE-TO-YYYYMMDD ( argument-1 [argument-2] )
(FUNCTION YEAR-TO-YYYY (YY, argument-2) * 10000 + nnnn) where:
YY = FUNCTION INTEGER (argument-1/10000)
nnnn = FUNCTION MOD (argument-1, 10000)
and where argument-1 of the INTEGER and MOD functions and argument-2 of the YEAR-TO-YYYY function are the same as argument-1 and argument-2 of the DATE-TO-YYYYMMDD function itself.
The DAY-OF-INTEGER function converts a date in the Gregorian calendar from integer date form to Julian date form (YYYYDDD). The type of this function is integer.
![]()
The DAY-TO-YYYYDDD function converts argument-1 from the form YYnnn to the form YYYYnnn. Argument-2, when added to the year at the time of execution, defines the ending year of a 100-year interval, or sliding window, into which the year of argument-1 falls. The type of this function is integer.
FUNCTION DAY-TO-YYYYDDD ( argument-1 [argument-2] )
(FUNCTION YEAR-TO-YYYY (YY, argument-2) * 1000 + nnn)
where:
YY = FUNCTION INTEGER (argument-1/1000)
nnn = FUNCTION MOD (argument-1, 1000)
and where argument-1 of the INTEGER and MOD functions and argument-2 of the YEAR-TO-YYYY functions are the same as argument-1 and argument-2 of the DAY-TO-YYYYDDD function itself.
![]()
The DISPLAY-OF function returns a character string containing the alphanumeric character representation - the external format representation - of the national characters in the argument.
The type of the function is alphanumeric.
![]()
![]()
The E function returns an approximation of e, the base of natural logarithms.
The type of the function is numeric.
![]()
2.718281828459045235
![]()
The EXP function returns an approximation of the value of e raised to the power of the argument.
The type of the function is numeric.
![]()
FUNCTION E ** argument-1
![]()
The EXP10 function returns an approximation of the value of 10 raised to the power of the argument.
The type of the function is numeric.
![]()
10 ** argument-1
The FACTORIAL function returns an integer that is the factorial of argument-1. The type of this function is integer.
![]()
![]()
The FRACTION-PART function returns a numeric value that is the fraction portion of the argument.
The type of the function is numeric.
![]()
(argument-1 - FUNCTION INTEGER-PART (argument-1))
where the argument for the INTEGER-PART function is the same as for the FRACTION-PART function itself.
Note: If the value of argument-1 is +1.5, +0.5 is returned. If the value of argument-1 is -1.5, -0.5 is returned.
The INTEGER function returns the greatest integer value that is less than or equal to the argument. The type of this function is integer.
![]()
The INTEGER-OF-DATE function converts a date in the Gregorian calendar from standard date form (YYYYMMDD) to integer date form. The type of this function is integer.
![]()
(YYYY * 10,000) + (MM * 100) + DD.
The INTEGER-OF-DAY function converts a date in the Gregorian calendar from Julian date form (YYYYDDD) to integer date form. The type of this function is integer.
![]()
(YYYY * 1000) + DDD.
The INTEGER-PART function returns an integer that is the integer portion of argument-1. The type of this function is integer.
![]()
The LENGTH function returns an integer equal to the length of the argument in alphanumeric character positions
![]() or national character
positions, depending on the class of the argument.
or national character
positions, depending on the class of the argument.
The type of this function is integer.
![]()
![]()
The LENGTH-AN function returns an integer equal to the length of the argument in number of alphnumeric character positions.
The type of the function is integer.
![]()
The LOG function returns a numeric value that approximates the logarithm to the base e (natural log) of argument-1. The type of this function is numeric.
![]()
The LOG10 function returns a numeric value that approximates the logarithm to the base 10 of argument-1. The type of this function is numeric.
![]()
The LOWER-CASE function returns a character string that is the same length as argument-1 with each uppercase letter replaced by the corresponding lowercase letter. The type of this function depends on the argument as follows:
| Argument Type |
Function Type |
|---|---|
| Alphabetic | Alphanumeric |
| Alphanumeric | Alphanumeric |
|
|
National |
![]()
![]() or national
or national
and must be at least one character in length.
The MAX function returns the content of the argument-1 that contains the maximum value. The type of this function depends upon the argument types as follows:
| Argument Type |
Function Type |
|---|---|
| Alphabetic | Alphanumeric |
| Alphanumeric | Alphanumeric |
|
|
National |
| All arguments integer | Integer |
| Numeric | Numeric |
| (some arguments can be integer) |
![]()
![]() or national
or national
the size of the returned value is the same as the size of the selected argument-1.
The MEAN function returns a numeric value that is the arithmetic mean (average) of its arguments. The type of this function is numeric.
![]()
The MEDIAN function returns the content of the argument whose value is the middle value in the list formed by arranging the arguments in sorted order. The type of this function is numeric.
![]()
The MIDRANGE (middle range) function returns a numeric value that is the arithmetic mean (average) of the values of the minimum argument and the maximum argument. The type of this function is numeric.
![]()
The MIN function returns the content of the argument-1 that contains the minimum value. The type of this function depends upon the argument types as follows:
| Argument Type |
Function Type |
|---|---|
| Alphabetic | Alphanumeric |
| Alphanumeric | Alphanumeric |
|
|
National |
| All arguments integer | Integer |
| Numeric | Numeric |
| (some arguments can be integer) |
![]()
![]() or national,
or national,
the size of the returned value is the same as the size of the selected argument-1.
The MOD function returns an integer value that is argument-1 modulo argument-2. The type of this function is integer.
![]()
argument-1 - (argument-2 * FUNCTION INTEGER (argument-1 / argument-2))
| Argument-1 |
Argument-2 |
Return |
|---|---|---|
| 11 | 5 | 1 |
| -11 | 5 | 4 |
| 11 | -5 | -4 |
| -11 | -5 | -1 |
![]()
The NATIONAL-OF function returns a character string containing the national character internal representation of the characters in the argument.
The type of the function is national.
![]()
The NUMVAL function returns the numeric value represented by the character string specified by argument-1. Leading and trailing spaces are ignored. The type of this function is numeric.
![]()
![]() or national
or national
literal or an alphanumeric
![]() or national
or national
data item whose content has one of the following two formats:
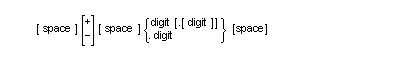
or
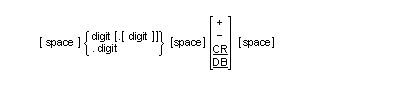
where space is a string of zero or more spaces and digit is a string of one to 18 digits.
The NUMVAL-C function returns the numeric value represented by the character string specified by argument-1. Any optional currency sign specified by argument-2 and any optional commas preceding the decimal point are ignored. The type of this function is numeric.
![]()
![]() or national
or national
literal or an alphanumeric
![]() or national
or national
data item whose content has one of the following two formats:

or
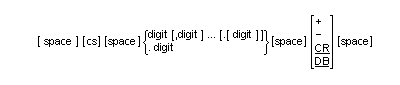
where space is a string of zero or more spaces, cs is the string of one or more characters specified by argument-2 and digit is a string of one or more digits.
It cannot be a digit, comma, space, plus sign(+), minus sign (-) or decimal point.
![]() ; or if argument-1 is of
class national, the national representation of the currency symbol
specified for the program. The national representation of cs is the
value returned from FUNCTION NATIONAL-OF (cs).
; or if argument-1 is of
class national, the national representation of the currency symbol
specified for the program. The national representation of cs is the
value returned from FUNCTION NATIONAL-OF (cs).
The ORD function returns an integer value that is the ordinal position of argument-1 in the collating sequence for the program. The lowest ordinal position is 1. The type of this function is integer.
![]()
![]() or national.
or national.
The ORD-MAX function returns a value that is the ordinal number of the argument-1 that contains the maximum value. The type of this function is integer.
![]()
The ORD-MIN function returns a value that is the ordinal number of the argument-1 that contains the minimum value. The type of this function is integer.

![]()
The PI function returns a value that is an approximation of, the ratio of the circumference of a circle to its diameter.
The type of the function is numeric.
![]()
3.141592653589793238
The PRESENT-VALUE function returns a value that approximates the present value of a series of future period-end amounts specified by argument-2 at a discount rate specified by argument-1. The type of this function is numeric.
![]()
argument-2 / (1+argument-1) ** n
There is one term for each occurrence of argument-2. The exponent, n, is incremented from one by one for each term in the series.
The RANDOM function returns a numeric value that is a pseudo-random number from a rectangular distribution. The type of this function is numeric.
![]()
The RANGE function returns a value that is equal to the value of the maximum argument minus the value of the minimum argument. The type of this function depends upon the argument types as follows:
| Argument Type |
Function Type |
|---|---|
| All arguments integer | Integer |
| Numeric | Numeric |
| (some arguments can be integer) |
![]()
The REM function returns a numeric value that is the remainder of argument-1 divided by argument-2. The type of this function is numeric.
![]()
argument-1 - (argument-2 * FUNCTION INTEGER-PART (argument-1 / argument-2))
The REVERSE function returns a character string whose length and characters are exactly the same as argument-1, except that the characters are in reverse order. The type of this function depends on the argument type as follows:
| Argument Type |
Function Type |
|---|---|
| Alphabetic | Alphanumeric |
| Alphanumeric | Alphanumeric |
|
|
National |
![]()
![]() or national
or national
and must be at least one character in length.
![]()
The SIGN function returns +1, 0, or -1 depending on the sign of the argument.
The type of the function is integer.
![]()
The SIN function returns a numeric value that approximates the sine of an angle or arc, expressed in radians, that is specified by argument-1. The type of this function is numeric.
![]()
Note: Conversion factors from degrees and Gon (grad) to radians are specified in the section Trigonometric Functions of this chapter.
The SQRT function returns a numeric value that approximates the square root of argument-1. The type of this function is numeric.
![]()
The STANDARD-DEVIATION function returns a numeric value that approximates the standard deviation of its arguments. The type of this function is numeric.
![]()
The SUM function returns a value that is the sum of the arguments. The type of this function depends upon the argument types as follows:
| Argument Type |
Function Type |
|---|---|
| All arguments integer | Integer |
| Numeric | Numeric |
| (some arguments may be integer) |
![]()
The TAN function returns a value that approximates the tangent of an angle or arc, expressed in radians, that is specified by argument-1. The type of this function is numeric.
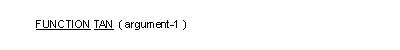
Note: Conversion factors from degrees and Gon (grad) to radians are specified in the section Trigonometric Functions of this chapter.
The UPPER-CASE function returns a character string that is the same length as argument-1 with each lowercase letter replaced by the corresponding uppercase letter. The type of this function depends on the argument as follows:
| Argument Type |
Function Type |
|---|---|
| Alphabetic | Alphanumeric |
| Alphanumeric | Alphanumeric |
|
|
National |
![]()
![]() or national
or national
and must be at least one character in length.
The VARIANCE function returns a numeric value that approximates the variance of its arguments. The type of this function is numeric.
![]()
The WHEN-COMPILED function returns the date and time the program was compiled. The type of this function is alphanumeric.

| Character Positions |
Contents |
|---|---|
| 1-4 | Four numeric digits of the year in the Gregorian calendar. |
| 5-6 | Two numeric digits of the month of the year, in the range 01 through 12. |
| 7-8 | Two numeric digits of the day of the month, in the range 01 through 31. |
| 9-10 | Two numeric digits of the hours past midnight, in the range 00 through 23. |
| 11-12 | Two numeric digits of the minutes past the hour, in the range 00 through 59. |
| 13-14 | Two numeric digits of the seconds past the minute, in the range 00 through 59. |
| 15-16 | Two numeric digits of the hundredths of a second
past the second, in the range 00 through 99.
If the system does not have the facility to provide fractional parts of a second, the value 00 is returned. |
| 17 | Either the character "–", the
character " +", or the character "0". The
character "–" is returned if the local time indicated
in the previous character positions is behind Greenwich Mean Time.
The character "+" is returned if the local time indicated
is the same or ahead of Greenwich Mean Time. The character "0"
is returned if the system on which this function is evaluated does
not have the facility to provide the local time differential factor.
If the system does not have the facility to provide the local time differential factor, the value 00000 is returned in character positions 17 through 21. |
| 18-19 | If character position 17 is "–", two numeric digits are returned in the range 00 through 12, indicating the number of hours that the reported time is behind Greenwich Mean Time. If character position 17 is "+", two numeric digits are returned in the range 00 through 13 indicating the number of hours that the reported time is ahead of Greenwich Mean Time. If character position 17 is "0", the value 00 is returned. |
| 20-21 | Two numeric digits are returned in the range 00
through 59 indicating the number of additional minutes that the
reported time is ahead of or behind Greenwich Mean Time, depending
on whether character position 17 is "+" or "–"
, respectively.
If character position 17 is "0", the value 00 is returned. |
The YEAR-TO-YYYY function converts argument-1, the two low-order digits of a year, to a four-digit year. Argument-2, when added to the year at the time of execution, defines the ending year of a 100-year interval, or sliding window, into which the year of argument-1 falls. The type of this function is integer.
FUNCTION YEAR-TO-YYYY ( argument-1 [argument-2] )
(FUNCTION NUMVAL (FUNCTION CURRENT-DATE (1:4)) + argument-2)
where argument-2 of the NUMVAL function is the same as argument-2 of the YEAR-TO-YYYY function itself.
(FUNCTION MOD (maximum-year, 100) > = argument-1)
The equivalent arithmetic expression is:
argument-1 + 100 * (FUNCTION INTEGER (maximum-year/100))
argument-1 + 100 * (FUNCTION INTEGER (maximum-year/100) - 1)
(fixed-maximum-year - FUNCTION NUMVAL (FUNCTION CURRENT-DATE (1:4)))
If the fixed window is 1973 through 2072, then in 2009 argument-2 has the value 63 and in 2019, the value 53.
Copyright © 1998 Micro Focus Limited. All rights reserved.
This document and the proprietary marks and names
used herein are protected by international law.
 | Procedure Division | Procedure Division - ACCEPT - DIVIDE |  |